|
The Fibonacci/Pascal Triangle hardware of brain:
| The cube's tetrahedron is the neuron processor. |
|
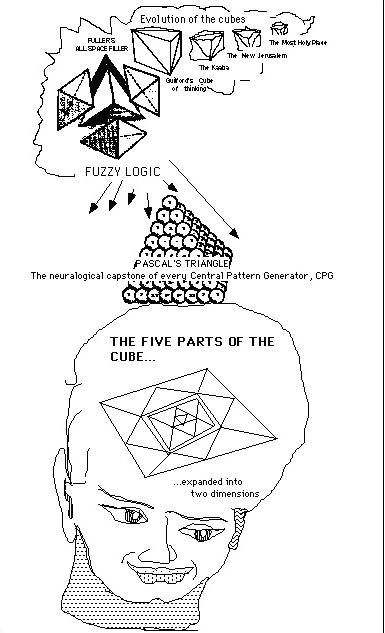
| The five geometries have physiological analogy with the brain |
Not everyone would care to read exactly how the neurons grow, through the process of cell mitosis, into a heirarchy of nerves
arranged in a binary organization relative to one another. For those who would like more details concerning the Fibonacci
growth pattern of mitosis, and the mathematical relationships between that series of neuron connections and Pascal's Triangle
of binary row alignments, get the KOFH publication, "Mindography, the one thing that explains understanding."
But, notice the 2-D format of the cube in the illustration above, it is important to our practical application of these
theories, particularly in regard to KOFH Academic Products for the K-12 Classroom and KOFH Educational Materials for Bible
Study.
Notice that, twelve large congruent triangles around the border of the square, actually frame another smaller square in
the center of the diagram. That smaller center square is analogous to the Central Pattern Generator, CPG, of the tetrahedronal
binary processor in our computer-like brain. A close look shows that this smaller square is further divided into congruent
triangles, also.
The twelve triangles which ring those in the center correspond to the twelve faces on the outside of the cube. The eight
triangles in the smaller center square correspond to the eight faces inside the cube. Each 2-D triangle corresponds one-to-one
with a triangular face on the 3-D cube. In this way, it becomes possible to represent the content of the three sets of numerically
grouped triangles. That content can be set down on paper and examined in a classroom setting. Hence, the theory lends itself
to educational pursuits which utilize the two concepts, the world of the Fuller "cubism" which can be understood
by the Mindography that explains it in our mind.
|

