|
The KOFH Publication, Mindography, presents the details. These few graphics suggest the main idea. The biology of a neurological
mass of cells growing together takes place by mitosis. These cells are the brain neurons. They maintain a direct contact
and association with one another as they develop, and they continue their association afterwards.
|
| (graphic links to more) |
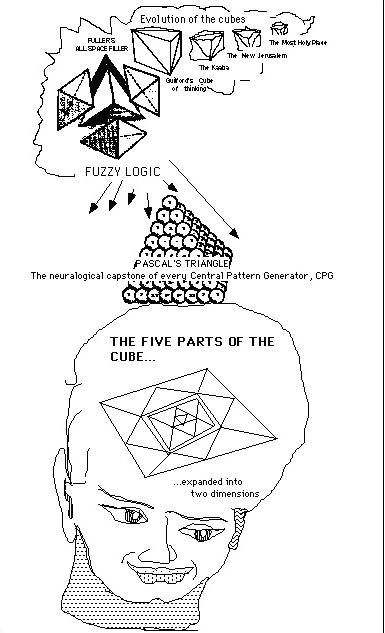
This growth process is in accord with the mathematics of the Fibonacci Series. The consequence of this math is the creation
of a Boolian Algebraic complex of transitor-like neurons. This is due to the mathematical relationship between Fibonacci
and Pascal. The neurons form a Pascal Triangular array.
This produces a ready binary relationship between the neurons of the brain. It is this binary array of neurons which
is the foundation of the Hardware that runs the Software of our thinking.
|

