Algebra I&II

This booklet covers both Algebra I and Algebra II

The course of study covers Linear Equations through Conic Sections

CLICK ON COVER ABOVE FOR MORE PRODUCT INFORMATION

"Buy one, make many"...
$29.99

This booklet contains the 16 templates that are to be photocopied and distributed to each student. Over the duration of the course, one page after another can be used to introduce new topics. When completed, each page is tucked inside the previous page creating a thick Lotus Flower type of notebook. Inside is a review of all the topics studied. It is a ready reference for Algebraic identities and transformations, and useful tool for review.

Sixteen (16) Lotus Leaf pages cover all the traditional topics found in High School Algebra II courses. The Lotus Leaf pages are organized in the same way as the text books so that these lessons are added to the normal presentations of the teachers, and are useful as a summary and a formal reference "notebook" to go back for reviews.

The sample lesson shown here offers an amazing addition to the traditional exercises involving Conic Sections.

The Algebra teachers will immediately see that the students can be taught to transpose from the standard equation for the Parabola to the other forms simply be exchanging the coefficients correctly, using the ready formulas to be found on this graphic organizer.

Of course, the exercises themselves have traditionally been used to make students practice the Alegbra required to discover the various properties. Teachers will not want to eliminate this exercise because it is essential to become proficient with the Algebra skills themselves.

But at some point the students are ready for this insight which allows them to quickly find roots and various varibles in a straight forward substitution as indicated in this Lotus Leaf Lesson.

Sample Lesson:

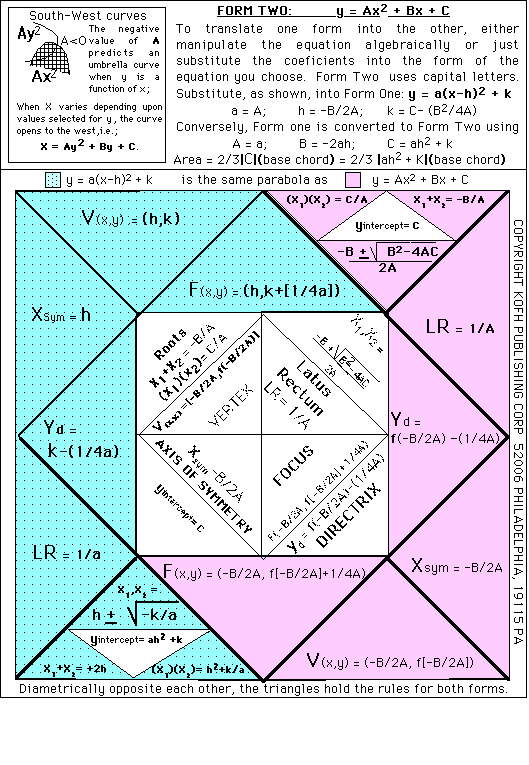
A close examination of the information on this sample Lotus Leaf page shows that students can learn how to transform between the two forms of the equation for a parabola. The various variables can easily be discovered by substitution of coefficients. The traditional work involved in transposing from one general equation into another in order to obtain the traditional coefficients used to find roots can be shortcut if this page is closely examined.

This reduces the work immensely.

The fact that this is possible but usually omitted from the standard text books not withstanding, this ought be a final lesson and useful double check on the Algebra. Such information and lessons are recommended after the traditional exercises are practiced.

The 16 Lotus pages cover the standard Algebra II text book chapters. This project-oriented-assignment is a break in the normal instructional routine. Lotus Leaf Algebra is not intended to replace traditional exercises and presentations, but is a supplemental set of lessons to reinforce and organize content The Lotus pages collect all the various identities into neat clear groupings. Students can be taught to use the notebook in order to find powers, roots, log transformations, etc.

Nevertheless, it is recommended that students are encouraged to attack Algebra assignments with these graphically organized pages of rules available to them as they work.

EACH PAGE FOLDS AND FINDS INSIDE THE LAST

A Review Lesson for manipulating Fractions, Decimals, and Percentages is also included. Transposing terms is one area of weakness which students bring to the Algebra Class. This method graphically represented below uses multiplication of the numerator and denominator in most all cases, and avoids the teaching of Lowest Common Denominators. This makes the "rules" rather straight forward, in the students are instructed to multiple in every case. The various possible exercises and required operations with mixed numbers and fractions, decimals, and percentage are show as examples below. Teachers ought find this useful double checking on student readiness before the Algebra Lessons are presented.

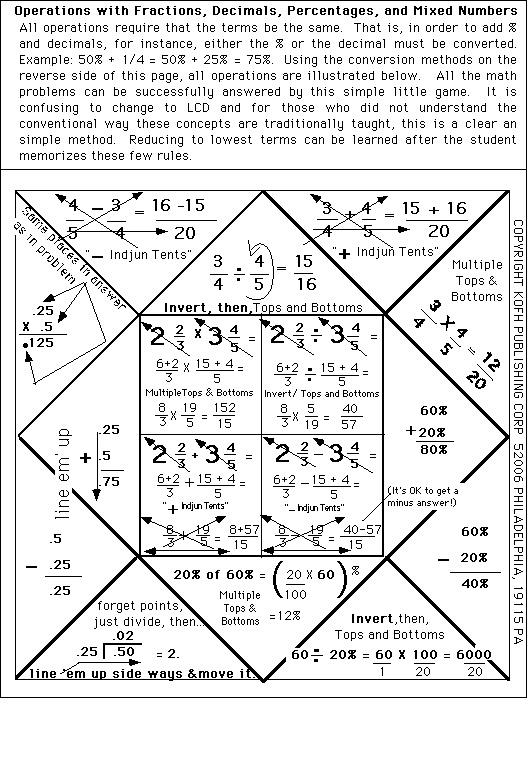
$fractions.jpg$

This review may be followed with algebraic examples like multiplying a/b X c/d and such exercises.

Examples like the following have been found beneficial to many students:

[X +(a/b)] - [Y+ (c/d)] = (Xb + a)/b - (Yd + c)]/d = d[(Xb + a)/bd- b[(Yd + c)]/bd

Enter supporting content here

CLICK ON LINKS BELOW FOR "HOW TO" INSTRUCTIONS FOR THESE PRODUCTS:

HOW TO UTILIZED THE HAND AS THE GRAPHIC ORGANIZER

HOW TO FOLD A PAGE IN THE LOTUS LEAF NOTEBOOK:

How TO USE THE BLACKBOARD TO LECTURE ON A LOTUS LEAF PAGE:

HOW TO CUT AND FOLD THE CUBES: